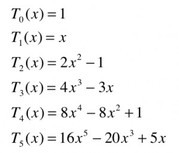Sound Design [under construction]
Conceptual Approach
DSP Approach
Tools Approach
Tools
Avid Protools HD 11
Apple Logic Studio X
Steinberg Cubase 6 & 7
Ableton Live 9 Suite
MaxMSP 6
Audiomulch 2
U&I Metasynth 5
CSound
NI Komplete 9
Spectrasonics Omnisphere
GRM Complete Tools
IRCAM Spat/Trax
Izotope
2C-Audio
Antares
Audio Damage
Brainworx
Celemony
D16
Drumatom
Fabfilter
Flux
Glitchmachines
McDSP
Melda
Ohmforce
The Plugin Alliance
Quikquak
Refuse
Softube
Sonalksis
Sonnox
Sonoris
Sound Radix
Soundtoys
Sugar Bytes
Tailored Noise
Triumph
Vengeance
Voxengo
WaveArts
Waves
XFER
Zynaptiq
DSP Approach
Tools Approach
Tools
Avid Protools HD 11
Apple Logic Studio X
Steinberg Cubase 6 & 7
Ableton Live 9 Suite
MaxMSP 6
Audiomulch 2
U&I Metasynth 5
CSound
NI Komplete 9
Spectrasonics Omnisphere
GRM Complete Tools
IRCAM Spat/Trax
Izotope
2C-Audio
Antares
Audio Damage
Brainworx
Celemony
D16
Drumatom
Fabfilter
Flux
Glitchmachines
McDSP
Melda
Ohmforce
The Plugin Alliance
Quikquak
Refuse
Softube
Sonalksis
Sonnox
Sonoris
Sound Radix
Soundtoys
Sugar Bytes
Tailored Noise
Triumph
Vengeance
Voxengo
WaveArts
Waves
XFER
Zynaptiq
Erin Coates - Merge (2013) [Video Art Piece: Composition, Field Recording/Sound Design, Surround Mix]
-Genre: Sound Art/Esoteric
-Genre: Sound Art/Esoteric
Distortion and Noise - Part One
In some areas of the industry, particularly those involved in the recording, mixing, and mastering of classical music, a knowledge of distortion and noise is critical in terms of eliminating the many different ways, both in the analog and digital domains, where an audio signal may be subject to degradation. The reason? Classical music is at an extremity of the audio engineering world where dynamic range, transparency, phase alignment, and the reproduction of sound stage and ambient space is absolutely critical. Factors like the total harmonic distortion (THD), intermodulation distortion, and signal-to-noise of various electronic components become most critical, and due to these factors many recording engineers of classical music will not compromise for anything but the best AD/DA converters, shielded and balanced cables, transformerless preamps, solid-state microphones with minimal signal-to-noise, passive EQ and/or [digital] 64-bit linear phase EQ, and minimal compression. A clean power supply is also critical. Engineers in this part of the industry are also ahead of the game when it comes to an awareness of dithering routines and the limitations that exist in PCM digital audio, shifting rather toward newer developments such as Sony/Phillips DSD (a dynamical 1-bit methodology called super-audio) and DXD (a sort-of “high-bandwidth” PCM) technology instead.
This awareness I would like to think is a necessity. However, perhaps not in opposition to this, other styles of music have, over many years, become dependent on distortion in its many forms, and consequently such effects have become intrinsic to these musical genres. Rock, metal, punk, grunge, doom, industrial, hardcore rave, and a huge number of stylistic derivatives have used various kinds of distortion to create a more unique and aggressive sonic palette. Distortion in some ways might be considered sonically as an “injection of attitude” as the process not only changes the tone of the signal, but also the dynamics – a kind of compression or squashing of the signal achieved by driving a signal at higher levels through valves, speaker cabinets, against tape et cetera. Terms like overdrive and saturation again relate to this fundamental idea of “squashing” the audio signal.
The more one delves into distortion, the more it appears to be a universe unto itself. From the most subtle harmonic distortion and coloration achieved when using analog electronic components like valve pre-amps and transformer based pre-amps, adjustments in input impedance and/or impedance mis-match, noisy components, different power supplies, to more extreme distortion achieved with FET transistors, overdriving speaker cabinets, valve distortion achieved when adjusting bias, tape saturation, and digital manipulation of phase and pulse-width, all the way through to extreme distortion involving signal rectification, noise modulation synthesis, waveshaping synthesis, signal truncation and rounding, signal bit-reduction, sample-rate reduction, logic bitwise and inequality operations. I generally consider these all as primarily “destructive” processes of signal modification.
When we hear the term distortion perhaps the first thing a lot of us think of is the sound of a distorted electric guitar. But the reality of distortion is that it exists in many different forms and extremities. Milder forms of signal distortion, what is referred to as harmonic distortion, is used in many cases as a way of “warming” or “fattening” a signal, for example when valves are used to add even harmonics, or tape saturation is used to accentuate odd harmonics in a signal. Distortion can also exist in more extreme forms where overdrive and signal rectification result in drastic tonal and dynamic changes in a signal. It often also decreases the signal-to-noise ratio, consequently accentuating the noisiness that exists in a signal. And noise in some ways has become, like distortion, an intrinsic aspect of our association with many contemporary styles of music.
Historically there has been a growing attraction to the use of noise in music composition and music performance. I believe John Cage was not far off the mark when he stated in 1937:
‘I believe that the use of noise to make music will continue and increase until we reach a music produced through the aid of electrical instruments which will make available for musical purposes any and all sounds that can be heard.’ — John Cage, The Future of Music: Credo (1937)
Edgard Varese’s Ionisation (1929-1931) and John Cage’s Cartridge Music (1960) were both influential works toward a growing trend in using noise (i.e. non-pitched sounds) as a central component of a composers sonic palette and compositional intent, as well as a performers artistic practice. This was most evident during the 1980’s when a new wave of noise artists and bands emerged including Merzbow and Ryuichi Sakamoto from Japan and Sonic Youth from the USA. Trent Reznor from Nine Inch Nails is another who has used noise, and also distortion, extensively in his own work – most notably among these practitioners is the use of different colorations of noise.
So where is all of this going? Well recently I have been starting to become more actively involved in live laptop performance, as well as ongoing work in sound design, mixing, and mastering at the studio. I have been actively building tools and instruments that allow me to be more creative both in the studio and in live situations. Teaching instrument design and sound synthesis has started to give me a different perspective on my own practice, and what kinds of sounds and modes of expression I wish to use. My aim has been to document these explorations as I go.
I have often found the creative process mysterious. What drives a creative artist toward an idea? In the case of a sound artist, toward a sound they might envisage? Well I saw Merzbow twice in Perth, and from then I became fascinated with not only noise, but methods of distortion, both analog and digital, and its infinite world both rich and full of possibilities. The difference between analog and digital processes became more apparent to me after using several analog distortion units here at the studio, whilst also practicing as a live laptop artist. I have three hardware units at the studio specifically designed for signal modification – the Evol Audio Fucifier, the Thermionic Culture Vulture (mastering edition), and the Sherman Filterbank. With this mix of valve and solid-state technology, each of these units can effectively generate rich and varied distortions of many different colors and varieties. I can also push these units to extremities, that seemed by comparison to software equivalents to have more “attitude” and “aggression”. By contrast I wanted to devise some methods I could use to “mangle” sounds in the digital world, and create a similar level of attitude. There is a universe of possible combinations and colors in both the analog and digital worlds. I am not going to argue what is better here between analog and digital, except to suggest that they are indeed different, and they should be judged individually based on the unique way in which each respective methodology modifies a signal. I am certainly not interested here in methods involving impulse responses and convolution synthesis aimed at the creation of digital emulations of analog gear. This article focusses specifically on some known digital methodologies aimed primarily at signal distortion, and to experiment to find some extended ways in which to use the computer to compute what it is best at computing: algorithms.
So in a way this write up focusses largely on a small combination of digital methodologies including noise modulation, waveshaping (including logic bitwise and inequality operations), phase distortion, and signal truncation and/or brickwall limiting.
1. Waveshaping
Waveshaping Synthesis is certainly one of the most widely used methods in signal distortion. This process involves running a waveform through a transfer function, and it is this transfer function that “reshapes” the input waveform. The only problem with waveshaping is that the technique can easily introduce aliasing – if you don’t know what that is, it is best to read about it. Most of the time it is best to avoid it. However, as we will see later in this article, we are also going to exploit its possibilities.
The mildest use of waveshaping synthesis is for the purposes of harmonic distortion (or the adding of harmonics). This is achieved through the use of Chebyshev functions of different order (N) as transfer functions. These allows us to generate frequencies up the Nth harmonic of the input waveform. This way we can ensure the highest frequency generated is below the nyquist frequency, hence avoiding aliasing. Each polynomial will generate a new harmonic, and these may be summed together as one likes – for example, to create the effect of introducing even or odd harmonics in a signal to model the coloration valves and tape impart on a signal.
The first five Chebyshev polynomials are:
This awareness I would like to think is a necessity. However, perhaps not in opposition to this, other styles of music have, over many years, become dependent on distortion in its many forms, and consequently such effects have become intrinsic to these musical genres. Rock, metal, punk, grunge, doom, industrial, hardcore rave, and a huge number of stylistic derivatives have used various kinds of distortion to create a more unique and aggressive sonic palette. Distortion in some ways might be considered sonically as an “injection of attitude” as the process not only changes the tone of the signal, but also the dynamics – a kind of compression or squashing of the signal achieved by driving a signal at higher levels through valves, speaker cabinets, against tape et cetera. Terms like overdrive and saturation again relate to this fundamental idea of “squashing” the audio signal.
The more one delves into distortion, the more it appears to be a universe unto itself. From the most subtle harmonic distortion and coloration achieved when using analog electronic components like valve pre-amps and transformer based pre-amps, adjustments in input impedance and/or impedance mis-match, noisy components, different power supplies, to more extreme distortion achieved with FET transistors, overdriving speaker cabinets, valve distortion achieved when adjusting bias, tape saturation, and digital manipulation of phase and pulse-width, all the way through to extreme distortion involving signal rectification, noise modulation synthesis, waveshaping synthesis, signal truncation and rounding, signal bit-reduction, sample-rate reduction, logic bitwise and inequality operations. I generally consider these all as primarily “destructive” processes of signal modification.
When we hear the term distortion perhaps the first thing a lot of us think of is the sound of a distorted electric guitar. But the reality of distortion is that it exists in many different forms and extremities. Milder forms of signal distortion, what is referred to as harmonic distortion, is used in many cases as a way of “warming” or “fattening” a signal, for example when valves are used to add even harmonics, or tape saturation is used to accentuate odd harmonics in a signal. Distortion can also exist in more extreme forms where overdrive and signal rectification result in drastic tonal and dynamic changes in a signal. It often also decreases the signal-to-noise ratio, consequently accentuating the noisiness that exists in a signal. And noise in some ways has become, like distortion, an intrinsic aspect of our association with many contemporary styles of music.
Historically there has been a growing attraction to the use of noise in music composition and music performance. I believe John Cage was not far off the mark when he stated in 1937:
‘I believe that the use of noise to make music will continue and increase until we reach a music produced through the aid of electrical instruments which will make available for musical purposes any and all sounds that can be heard.’ — John Cage, The Future of Music: Credo (1937)
Edgard Varese’s Ionisation (1929-1931) and John Cage’s Cartridge Music (1960) were both influential works toward a growing trend in using noise (i.e. non-pitched sounds) as a central component of a composers sonic palette and compositional intent, as well as a performers artistic practice. This was most evident during the 1980’s when a new wave of noise artists and bands emerged including Merzbow and Ryuichi Sakamoto from Japan and Sonic Youth from the USA. Trent Reznor from Nine Inch Nails is another who has used noise, and also distortion, extensively in his own work – most notably among these practitioners is the use of different colorations of noise.
So where is all of this going? Well recently I have been starting to become more actively involved in live laptop performance, as well as ongoing work in sound design, mixing, and mastering at the studio. I have been actively building tools and instruments that allow me to be more creative both in the studio and in live situations. Teaching instrument design and sound synthesis has started to give me a different perspective on my own practice, and what kinds of sounds and modes of expression I wish to use. My aim has been to document these explorations as I go.
I have often found the creative process mysterious. What drives a creative artist toward an idea? In the case of a sound artist, toward a sound they might envisage? Well I saw Merzbow twice in Perth, and from then I became fascinated with not only noise, but methods of distortion, both analog and digital, and its infinite world both rich and full of possibilities. The difference between analog and digital processes became more apparent to me after using several analog distortion units here at the studio, whilst also practicing as a live laptop artist. I have three hardware units at the studio specifically designed for signal modification – the Evol Audio Fucifier, the Thermionic Culture Vulture (mastering edition), and the Sherman Filterbank. With this mix of valve and solid-state technology, each of these units can effectively generate rich and varied distortions of many different colors and varieties. I can also push these units to extremities, that seemed by comparison to software equivalents to have more “attitude” and “aggression”. By contrast I wanted to devise some methods I could use to “mangle” sounds in the digital world, and create a similar level of attitude. There is a universe of possible combinations and colors in both the analog and digital worlds. I am not going to argue what is better here between analog and digital, except to suggest that they are indeed different, and they should be judged individually based on the unique way in which each respective methodology modifies a signal. I am certainly not interested here in methods involving impulse responses and convolution synthesis aimed at the creation of digital emulations of analog gear. This article focusses specifically on some known digital methodologies aimed primarily at signal distortion, and to experiment to find some extended ways in which to use the computer to compute what it is best at computing: algorithms.
So in a way this write up focusses largely on a small combination of digital methodologies including noise modulation, waveshaping (including logic bitwise and inequality operations), phase distortion, and signal truncation and/or brickwall limiting.
1. Waveshaping
Waveshaping Synthesis is certainly one of the most widely used methods in signal distortion. This process involves running a waveform through a transfer function, and it is this transfer function that “reshapes” the input waveform. The only problem with waveshaping is that the technique can easily introduce aliasing – if you don’t know what that is, it is best to read about it. Most of the time it is best to avoid it. However, as we will see later in this article, we are also going to exploit its possibilities.
The mildest use of waveshaping synthesis is for the purposes of harmonic distortion (or the adding of harmonics). This is achieved through the use of Chebyshev functions of different order (N) as transfer functions. These allows us to generate frequencies up the Nth harmonic of the input waveform. This way we can ensure the highest frequency generated is below the nyquist frequency, hence avoiding aliasing. Each polynomial will generate a new harmonic, and these may be summed together as one likes – for example, to create the effect of introducing even or odd harmonics in a signal to model the coloration valves and tape impart on a signal.
The first five Chebyshev polynomials are:
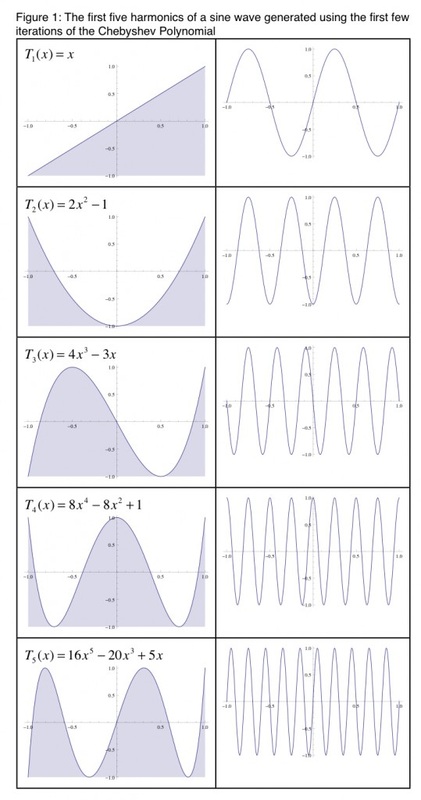
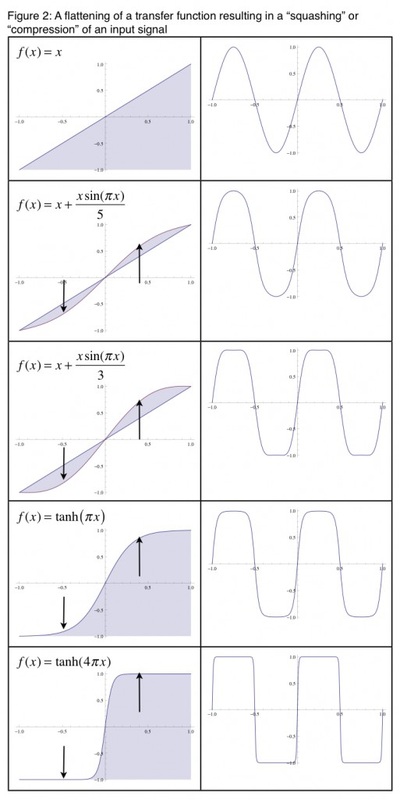
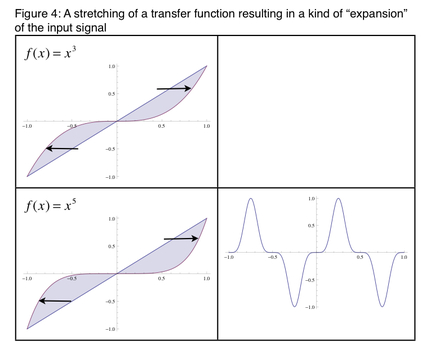
A second approach to using waveshaping which is again widely documented is the simulating of overdrive. This is achieved with an overall flattening of the transfer function. In the following set of images, we can see what each transfer function does by observing the shape of the respective waveform. As we move through these series of transfer functions, we can see a general flattening of the waveform. In a way we find the process acts as a compressor on the signal, but not in a conventional way!
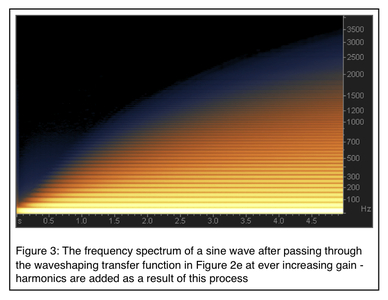
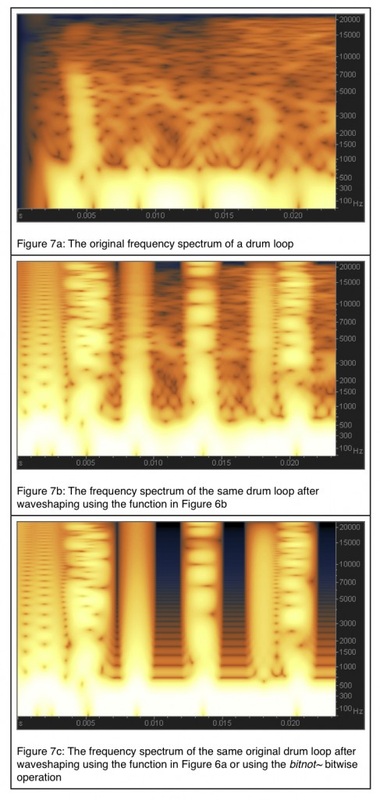
As we increase the input gain we find the transfer function introduces further harmonics. We can see the process unfolding in the following spectrogram where time passes from left to right. We see new harmonics enter as the gain of the input signal is increased before running through the hyperbolic tangent transfer function.
We can also reverse the effect, similar as to what we might find in signal expansion, by bending the transfer function in the opposite direction.
One of the primary observations I have made from the work of Merzbow is the minimal dynamic range – sounds are generally at the maximum threshold. The distortions are also more extreme, to the point where the sound source is rarely determinate. Could we also say that aliasing is a factor to be encouraged here? Extreme aliasing would certainly go a long way to obscuring the timbral and spectral qualities inherent in a sound source. I hope so, because some of the following examples are going to exploit this!
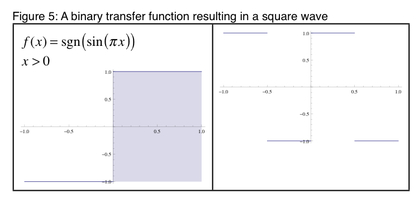
Lets suggest some possibilities here, as since there is minimal dynamic fluctuation it might also imply lower bit-depths. You could say that if it were possible to overdrive a speaker to the point where it would completely flatten a waveform, it would result in a square wave! (Figure 5). This is also analogous to converting a digital signal to 1-bit PCM signal. Mathematically a square wave can also be generated from a sine wave using the sgn function. It can also be achieved using an inequality like “greater than” or “less than”. This kind of signal is hardly possible to generate in the real physical world. The binary nature of this seems to me to be something computers are naturally adept at, and does not come naturally to the analog world without the use of digital components.
Lets suggest some possibilities here, as since there is minimal dynamic fluctuation it might also imply lower bit-depths. You could say that if it were possible to overdrive a speaker to the point where it would completely flatten a waveform, it would result in a square wave! (Figure 5). This is also analogous to converting a digital signal to 1-bit PCM signal. Mathematically a square wave can also be generated from a sine wave using the sgn function. It can also be achieved using an inequality like “greater than” or “less than”. This kind of signal is hardly possible to generate in the real physical world. The binary nature of this seems to me to be something computers are naturally adept at, and does not come naturally to the analog world without the use of digital components.
Well, in fact, a square wave only consists of odd integer harmonics as opposed to the sawtooth wave which contains all integer harmonics. So rather than a speaker amp, using this transfer function would be like slamming a signal against tape at an infinite level. Ok that’s not going to happen! And the tape medium would impart its own color and sound anyway, including inherent effects such as wow and flutter.
Lets say that based on this example, we want to turn some of this theory on its head, and what it is we want to achieve in terms of dynamics and tone shaping. We are not going to rule out aliasing. And we are not aiming here to emulate the behavior of valve and speaker components, but rather we want to find distortion methods that are unique to digital processes. I would argue that for some noise artists, it is most critical to “reveal” the noise in a signal. In fact noise is quite common. In mastering, dithering is a process where a small amount of noise is injected into an audio signal to randomize the quantization error created when a file is converted from a higher bit-depth to a lower bit-depth. This is used to avoid the possibility of periodic limit cycles.
Noise is also common on analog signal path. All electronic components exhibit a certain amount of noise. Studio equipment will always have a rating based on their own signal-to-noise ratio.
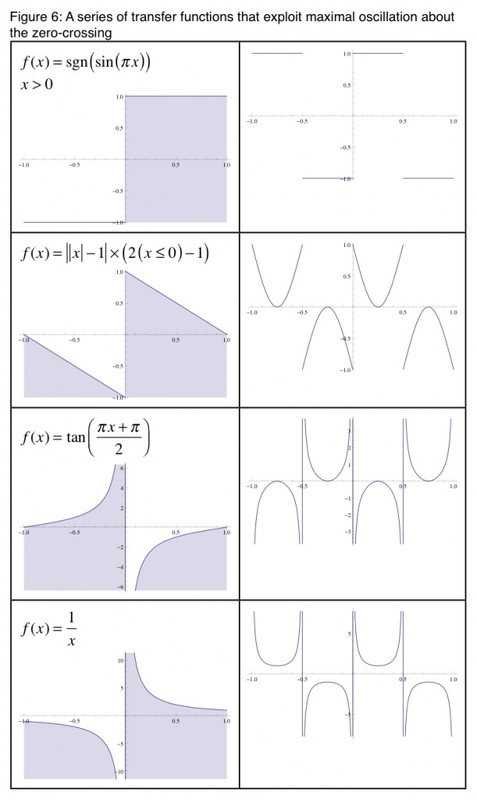
So how do we “reveal” this noise in a signal? Well we can achieve this by using a waveshaping transfer function where the minimum and maximum peaks occur about the zero-crossing. This kind of transfer function will have the effect of maximising low level fluctuation in the signal. The square wave is one such example, but what other functions have this characteristic about the zero crossing? Refer to Figure 6 for a list. Please note some of these transfer functions result in a waveform that exceeds the -1, +1 domain range, so will require a limiter.
Having the maximal peak and trough about where the zero-crossing normally occurs changes many of the inherent characteristics of the source wave, including the way in which dynamics are perceived. There are some other transfer functions that result in a maximum and minimum around the zero-crossing. For example, logic bitwise operation bit NOT is one.
Lets say that based on this example, we want to turn some of this theory on its head, and what it is we want to achieve in terms of dynamics and tone shaping. We are not going to rule out aliasing. And we are not aiming here to emulate the behavior of valve and speaker components, but rather we want to find distortion methods that are unique to digital processes. I would argue that for some noise artists, it is most critical to “reveal” the noise in a signal. In fact noise is quite common. In mastering, dithering is a process where a small amount of noise is injected into an audio signal to randomize the quantization error created when a file is converted from a higher bit-depth to a lower bit-depth. This is used to avoid the possibility of periodic limit cycles.
Noise is also common on analog signal path. All electronic components exhibit a certain amount of noise. Studio equipment will always have a rating based on their own signal-to-noise ratio.
So how do we “reveal” this noise in a signal? Well we can achieve this by using a waveshaping transfer function where the minimum and maximum peaks occur about the zero-crossing. This kind of transfer function will have the effect of maximising low level fluctuation in the signal. The square wave is one such example, but what other functions have this characteristic about the zero crossing? Refer to Figure 6 for a list. Please note some of these transfer functions result in a waveform that exceeds the -1, +1 domain range, so will require a limiter.
Having the maximal peak and trough about where the zero-crossing normally occurs changes many of the inherent characteristics of the source wave, including the way in which dynamics are perceived. There are some other transfer functions that result in a maximum and minimum around the zero-crossing. For example, logic bitwise operation bit NOT is one.
2. Phase Distortion, Pulse-Width Modulation, and signal Rectification
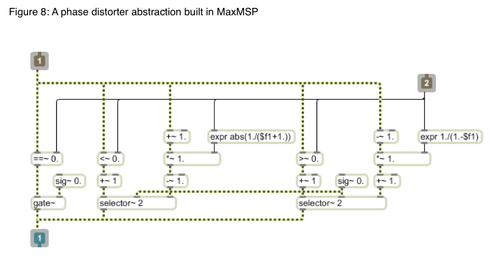
For standard oscillators, implementing phase distortion on a signal can be achieved in MaxMSP using the kink~ object. However this will only help us when we are distorting the phase of a table lookup oscillator. In order to distort the phase or pulse-width of any signal we must change where the zero-crossing occurs in the waveform. This can be achieved in several ways. The method shown in the MaxMSP patch below describes a process centered yet again around waveshaping. This example uses a waveshape where the zero crossing can be shifted left or right within the domain -1 and +1, causing a distortion in the overall waveform. The maximum and minimum peaks in the waveform remain relative to the original waveform, however the perceived dynamic intensity of the signal is compromised due to an incurred DC offset. The relative distance of the maximal and minimal peak values to the DC offset is what effects the overall perceived dynamic intensity.
For standard oscillators, implementing phase distortion on a signal can be achieved in MaxMSP using the kink~ object. However this will only help us when we are distorting the phase of a table lookup oscillator. In order to distort the phase or pulse-width of any signal we must change where the zero-crossing occurs in the waveform. This can be achieved in several ways. The method shown in the MaxMSP patch below describes a process centered yet again around waveshaping. This example uses a waveshape where the zero crossing can be shifted left or right within the domain -1 and +1, causing a distortion in the overall waveform. The maximum and minimum peaks in the waveform remain relative to the original waveform, however the perceived dynamic intensity of the signal is compromised due to an incurred DC offset. The relative distance of the maximal and minimal peak values to the DC offset is what effects the overall perceived dynamic intensity.
This phase distortion or pulse-width modulation is useful when combined with another distortion process. And when we are using a square wave as our transfer function, we can more efficiently perform phase distortion or pulse-width modulation with a comparator like the > or < inequalities, and change the argument from between -1 and +1. For example, x > 0 will result in a different pulse-width than the inequality x > 0.1.
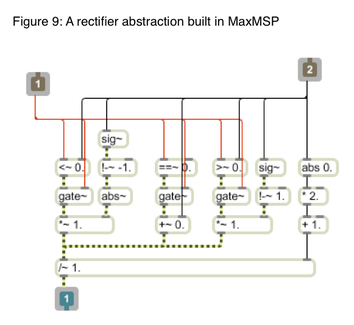
Not too dissimilar to our first example of phase distortion, we have an example below that shows how we may implement rectification of a signal. This algorithm creates significant changes in the resulting waveform.
Not too dissimilar to our first example of phase distortion, we have an example below that shows how we may implement rectification of a signal. This algorithm creates significant changes in the resulting waveform.
This process designed here changes the weighting of the waveform in the positive or negative direction (in terms of DC offset). Like in the previous examples, there is some change in the phase or pulse-width of the waveform, but a “rectification” of the signal is evident also. By removing the DC offset with a high-pass filter can bring the signal back to an oscillation about the zero-crossing.
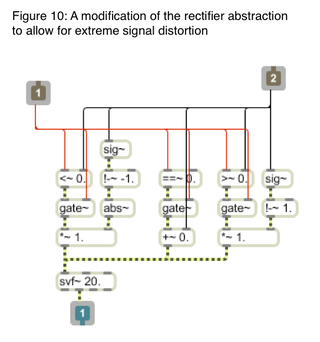
However I did find I could also use this method for more extreme methods of distortion on a signal. With a slight variation on this MaxMSP patch, this following example I could push with values between -10000 and +10000 provided a DC offset filter (high pass) filter is applied. To control the dynamics this also needs to be run through a limiter or a hyperbolic tangent function. This has become one of my preferred methods of signal distortion.
However I did find I could also use this method for more extreme methods of distortion on a signal. With a slight variation on this MaxMSP patch, this following example I could push with values between -10000 and +10000 provided a DC offset filter (high pass) filter is applied. To control the dynamics this also needs to be run through a limiter or a hyperbolic tangent function. This has become one of my preferred methods of signal distortion.
3. Noise Modulation
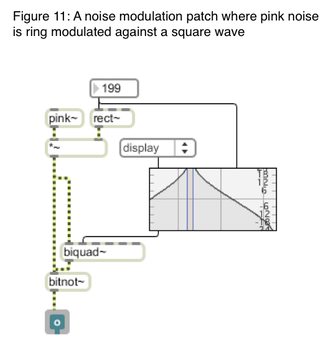
The concept of noise modulation is where we modulate a signals frequency, amplitude, or phase according to a noisy signal. Generally signals with an equal weighting across all frequency bands does not give effective results, but noisy signals with different weighting curves are significantly more effective. There are different colors of noise – white, pink, red (brownian), blue, violet, and grey. Each of these different colors of noise has a different associated weighting curve. White noise for instance has an equal weighting curve for all frequencies across the spectrum. So for noise modulation I would generally recommend pink, red, blue, violet, and grey noise. For example, here is pink noise ring modulated with a square wave:
The concept of noise modulation is where we modulate a signals frequency, amplitude, or phase according to a noisy signal. Generally signals with an equal weighting across all frequency bands does not give effective results, but noisy signals with different weighting curves are significantly more effective. There are different colors of noise – white, pink, red (brownian), blue, violet, and grey. Each of these different colors of noise has a different associated weighting curve. White noise for instance has an equal weighting curve for all frequencies across the spectrum. So for noise modulation I would generally recommend pink, red, blue, violet, and grey noise. For example, here is pink noise ring modulated with a square wave:
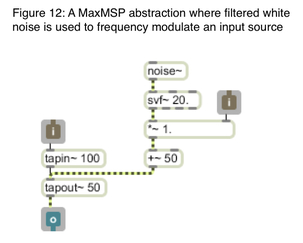
And here is white noise being used to modulate the frequency of an input:
4. Hard Limiting vs Soft Limiting
Another handy tool for the laptop noise artist is the brickwall limiter, which implements soft clipping, and a second technique referred to as signal truncation or hard clipping. Both of these techniques effectively have an attack time of zero, and both keep a signal within the ceiling 0dbfs. However both techniques will impart harmonics on a signal. Hard clipping results in aliasing, and soft clipping will not. The brickwall limiter is often used only for mastering in order to increase the perceived level of audio. However in live performance we might want to consider these tools quite differently, and what role they might play.
Some of the techniques that are described in mastering go through the role of the brickwall limiter and how to compensate for too much bottom end, by boosting the top end and vice versa. The brickwall limiter is something one can stack audio against, and the more you push any particular sound, the more it emerges. The technique becomes more coloristic and timbral, as the performer can then sculpt the spectrum by adjusting the qualities and timbre of each instrumental layer. So by pushing a sound in level hard against the limiter will have the perceived effect of pushing other sounds out of the mix, and also consequently increasing the harmonic content of that particular sound. This is not something I advise in any normal circumstances, and I would proceed with caution! All I will say is the EQing your layers is recommended, and bandpass EQ curves here are your friend.
5. Conclusion
So to wrap some of this up, some of my recent laptop noise work has incorporated principals and ideas I have documented here. As far as musical “devices” are concerned, I wanted to outline some of the methods I have used to create more aggressive and abrasive sounds. Waveshaping is without a doubt one of the most significant tools, but I have documented some ideas and suggestions as to how phase distortion, signal rectification, noise modulation, and the brickwall limiter can also be used.
Another handy tool for the laptop noise artist is the brickwall limiter, which implements soft clipping, and a second technique referred to as signal truncation or hard clipping. Both of these techniques effectively have an attack time of zero, and both keep a signal within the ceiling 0dbfs. However both techniques will impart harmonics on a signal. Hard clipping results in aliasing, and soft clipping will not. The brickwall limiter is often used only for mastering in order to increase the perceived level of audio. However in live performance we might want to consider these tools quite differently, and what role they might play.
Some of the techniques that are described in mastering go through the role of the brickwall limiter and how to compensate for too much bottom end, by boosting the top end and vice versa. The brickwall limiter is something one can stack audio against, and the more you push any particular sound, the more it emerges. The technique becomes more coloristic and timbral, as the performer can then sculpt the spectrum by adjusting the qualities and timbre of each instrumental layer. So by pushing a sound in level hard against the limiter will have the perceived effect of pushing other sounds out of the mix, and also consequently increasing the harmonic content of that particular sound. This is not something I advise in any normal circumstances, and I would proceed with caution! All I will say is the EQing your layers is recommended, and bandpass EQ curves here are your friend.
5. Conclusion
So to wrap some of this up, some of my recent laptop noise work has incorporated principals and ideas I have documented here. As far as musical “devices” are concerned, I wanted to outline some of the methods I have used to create more aggressive and abrasive sounds. Waveshaping is without a doubt one of the most significant tools, but I have documented some ideas and suggestions as to how phase distortion, signal rectification, noise modulation, and the brickwall limiter can also be used.